Get Latest Exam Updates, Free Study materials and Tips

1. The axis of precession is ____________ to the plane in which the axis of spin is going to rotate.
a) parallel
b) perpendicular
c) spiral
d) none of the mentioned
Answer: b
Explanation: The axis of precession is perpendicular to the plane in which the axis of spin is going to rotate. The gyroscopic principle is used in an instrument or toy known as gyroscope.
2. A disc is a spinning with an angular velocity ω rad/s about the axis of spin. The couple applied to the disc causing precession will be
a) 1/2 Iω2
b) Iω2
c) 1/2 Iωωp
d) Iωωp
Answer: d
Explanation: None
3. The engine of an aeroplane rotates in clockwise direction when seen from the tail end and the aeroplane takes a turn to the left. The effect of gyroscopic couple on the aeroplane will be
a) to dip the nose and tail
b) to raise the nose and tail
c) to raise the nose and dip of the tail
d) to dip the nose and raise the tail
Answer: c
Explanation: The engine of an aeroplane rotates in clockwise direction when seen from the tail end and the aeroplane takes a turn to the left. The effect of gyroscopic couple on the aeroplane will be to raise the nose and dip of the tail.
The engine of an aeroplane rotates in clockwise direction when seen from the tail end and the aeroplane takes a turn to the right. The effect of gyroscopic couple on the aeroplane will be to dip the nose and raise the tail.
4. The engine of an aeroplane rotates in clockwise direction when seen from the tail end and the aeroplane takes a turn to the right. The effect of gyroscopic couple on the aeroplane will be to dip the nose and raise the tail.
a) True
b) False
Answer: a
Explanation: The engine of an aeroplane rotates in clockwise direction when seen from the tail end and the aeroplane takes a turn to the left. The effect of gyroscopic couple on the aeroplane will be to raise the nose and dip of the tail.
The engine of an aeroplane rotates in clockwise direction when seen from the tail end and the aeroplane takes a turn to the right. The effect of gyroscopic couple on the aeroplane will be to dip the nose and raise the tail.
5. The steering of a ship means
a) movement of a complete ship up and down in vertical plane about transverse axis
b) turning of a complete ship in a curve towards right or left, while it moves forward
c) rolling of a complete ship side-ways
d) none of the mentioned
Answer: b
Explanation: The steering is the turning of a complete ship in a curve towards right or left, while it moves forward.
6. The rolling of a complete ship side-ways is known as pitching of a ship.
a) True
b) False
Answer: b
Explanation: The pitching is the movement of a complete ship up and down in a vertical plane about transverse axis.
7. The rotor of a ship rotates in clockwise direction when viewed from stern and the ship takes a left turn. The effect of gyroscopic couple acting on it will be
a) to raise the bow and stern
b) to lower the bow and stern
c) to raise the bow and lower the stern
d) to raise the stern and lower the bow
Answer: c
Explanation: The rotor of a ship rotates in clockwise direction when viewed from stern and the ship takes a left turn. The effect of gyroscopic couple acting on it will be to raise the bow and lower the stern.
The rotor of a ship rotates in clockwise direction when viewed from stern and the ship takes a right turn. The effect of gyroscopic couple acting on it will be to raise the stern and lower the bow.
8. The rotor of a ship rotates in clockwise direction when viewed from stern and the ship takes a right turn. The effect of gyroscopic couple acting on it will be to raise the stern and lower the bow.
a) True
b) False
Answer: a
Explanation: The rotor of a ship rotates in clockwise direction when viewed from stern and the ship takes a left turn. The effect of gyroscopic couple acting on it will be to raise the bow and lower the stern.
The rotor of a ship rotates in clockwise direction when viewed from stern and the ship takes a right turn. The effect of gyroscopic couple acting on it will be to raise the stern and lower the bow.
9. The pitching of a ship is assumed to take place with simple harmonic motion.
a) True
b) False
Answer: a
Explanation: None.
10. When the pitching of a ship is upward, the effect of gyroscopic couple acting on it will be
a) to move the ship towards star-board
b) to move the ship towards port side
c) to raise the bow and lower the stern
d) to raise the stern and lower the bow
Answer: a
Explanation: When the pitching of a ship is upward, the effect of gyroscopic couple acting on it will be to move the ship towards star-board.
When the pitching of a ship is downward, the effect of gyroscopic couple, is to turn the ship towards port side.
11) Calculate gyroscopic couple acting on a disc which has radius of 135 mm. Angular and precessional velocities are 15 rad/sec and 7 rad/sec respectively.
Assume density = 7810 kg/m3 and thickness of disc = 30 mm
a. 12.83 N-m
b. 10.99 N-m
c. 11 N-m
d. Incomplete data
ANSWER: 12.83 N-m
12) Gyroscopic effect is not observed in which of the following actions performed by the ships?
a. Rolling
b. Pitching
c. Steering
d. All of the above
ANSWER: Rolling
13) What is meant by pitching of ship?
a. up and down motion of bow and stern along transverse axis
b. up and down motion of bow and stern along longitudinal axis
c. up and down motion of port and starboard along transverse axis
d. none of the above
ANSWER: up and down motion of bow and stern along transverse axis
14) Calculate reactive gyroscopic couple acting on rotating disc which is inclined at an angle of 1.5o. Mass moment of inertia about polar and diametral axis is 2.45 kg-m2 and 0.5 kg-m2 respectively. The disc rotates at an angular velocity of 130 rad/sec
a. 800.36 N-m
b. 862.36 N-m
c. 850.11 N-m
d. None of the above
ANSWER: 862.36 N-m
15) What is the effect of reactive gyroscopic couple when aeroplane takes right turn and propeller rotates in clockwise direction?
a. The tail of the aeroplane is dipped and nose is raised
b. The tail of the aeroplane is raised and nose is dipped
c. Reactive gyroscopic couple has no effect when propeller rotates in clockwise direction
d. None of the above
ANSWER: The tail of the aeroplane is raised and nose is dipped
16) What is the effect of reactive gyroscopic couple when an aeroplane takes a right turn and propeller rotates in anticlockwise direction?
a. The nose and tail of the aeroplane are in horizontal plane
b. The nose of the aeroplane is raised and tail is dipped
c. The nose of the aeroplane is dipped and tail is raised
d. None of the above
ANSWER: The nose of the aeroplane is dipped and tail is raised
17) What is the gyroscopic couple acting on the disc which has mass moment of inertia equal to 0.02135 kg-m2. If disc has a speed of 500 rpm and is made to precess at 100 rpm.
a. 13.21 N-m
b. 11.70 N-m
c. 10.23 N-m
d. Incomplete data
ANSWER: 11.70 N-m
18) Which of the following statements is/are false for active gyroscopic couple?
a. Reactive gyroscopic couple and active gyroscopic couple are opposite in direction
b. In right hand rule, curled fingers denote direction of precession
c. In active gyroscopic couple spin vector and precession vector are parallel to each other
d. All the statements are false
Answer Explanation
ANSWER: In active gyroscopic couple spin vector and precession vector are parallel to each other
19) How is the direction of precession vector decided by right hand rule?
a. Thumb denotes direction of precession vector
b. Curled fingers denote direction of precession vector
ANSWER: Thumb denotes direction of precession vector
20) Degree of freedom for gyroscope rotor is
a. 1
b. 2
c. 3
d. 5
Answer Explanation
ANSWER: 3
21.A reverted gear train is one in which the output and input shaft:
(A) Rotates in opposite directions
(B) Are co-axial
(C) Are at right angles to each other
(D) None
ANSWERS:B
13-When two spur gears having involute profiles on their teeth engage the line of action is tangential to:
(A) Pitch circle
(B) Dedundum circle
(C) Addendum circle
(D) Base circle
ANSWERS:A
14-A worm has a lead angle of 22.5°. This corresponds to a helix angle of:
(A) 22.5°
(B) 45°
(C) 55°
(D) 67.5°
ANSWERS:D
15-Which of the following is not a friction clutch?
(A) Plate clutch
(B) Jaw clutch
(C) Cone clutch
(D) Centrifugal clutch
ANSWERS:B
16-Generally, there are ___ types of belts.
(A) One
(B) Two
(C) Three
(D) Four
ANSWERS:D
17-Which gear is used for power transmission in parallel shafts?
(A) Worm gear
(B) Rack and pinion
(C) Helical gear
(D) Bevel gear
ANSWERS:C
18-In spur gear of pitch diameter=168mm, module=3.5mm, the number of teeth will be
(A) 48
(B) 24
(C) 72
(D) 96
ANSWERS:A
19-In a spur gear the pitch diameter 40mm, outside diameter 48 mm, module 4 mm, the number of teeth will be
(A) 10 teeth
(B) 20 teeth
(C) 30 teeth
(D) 40 teeth
ANSWERS:A
20-The distance between two corresponding points of a teeth is known as
(A) Margin
(B) Lead
(C) Pitch
(D) None
ANSWERS:C
21-If the equilibrium speed of a governor is constant for all radii of rotation of the fly balls within the working range, it is known as
(A) Isochronism
(B) Hunting
(C) Insensitiveness
(D) Stability
ANSWERS:A
22-The gyroscopic couple of a suspended disc rotating at 1000 rpm is 15 N-m and the moment of inertia is 0.4 kg-m2, then the precession velocity of the disc in rad/sec is close to
(A) 0.35
(B) 35
(C) 8.5
(D) 0.0375
ANSWERS:A
23. The height of a Watt’s governor is equal to
a) 8.95/N2
b) 89.5/N2
c) 895/N2
d) 8950/N2
Answer: c
Explanation: If N is the speed of the arm and ball about the spindle axis, then the height of the governor (h) is given by
h = 895/N2 metres
24. The height of a Watt’s governor is
a) directly proportional to speed
b) directly proportional to (speed)
c) inversely proportional to speed
d) inversely proportional to (speed)
Answer: d
Explanation: If N is the speed of the arm and ball about the spindle axis, then the height of the governor (h) is given by
h = 895/N2 metres
From this expression, we see that the height height of a Watt’s governor is inversely proportional to N2
25. A Watt’s governor can work satisfactorily at speeds from
a) 60 to 80 r.p.m
b) 80 to 100 r.p.m
c) 100 to 200 r.p.m
d) 200 to 300 r.p.m
Answer: a
Explanation: A watt’s governor may only work satisfactorily at low speeds i.e. from 60 to 80 r.p.m.
26. The ratio of height of Porter governor to the height of Watt’s governor is
a) m/m + M
b) M/ m + M
c) m + M/m
d) m + M/M
Answer: c
Explanation: The ratio of height of a Porter governor (when length of arms and links are equal) to the height of Watt’s governor is m + M/n, where m and M re the masses of the ball and sleeve respectively.
27. When the sleeve of a porter governor moves upwards, the governor speed
a) increases
b) decreases
c) remains unaffected
d) first increases and then decreases
Answer: a
Explanation: When the sleeve of a porter governor moves upwards, the governor speed increases and when the sleeve moves downwards, the governor speed decreases.
28. When the sleeve of a Porter governor moves downwards, the governor speed
a) increases
b) decreases
c) remains unaffected
d) first increases and then decreases
Answer: b
Explanation: When the sleeve of a porter governor moves upwards, the governor speed increases and when the sleeve moves downwards, the governor speed decreases.
29. In a Porter governor, the balls are attached to the extension of lower links.
a) True
b) False
Answer: a
Explanation: Porter governor is a modification of Watt’s governor, with a central load attached to the sleeve.
30. A Hartnell governor is a
a) dead weight governor
b) pendulum type governor
c) spring loaded governor
d) inertia governor
Answer: c
Explanation: A Hartnell governor is a spring loaded governor.
31.Watt’s governor is a pendulum type governor.
a) True
b) False
Answer: b
Explanation: A Hartnell governor is a spring loaded governor.
Watt’s governor is a pendulum type governor.
32. Which of the following is a pendulum type governor?
a) Watt’s governor
b) Porter governor
c) Hartnell governor
d) None of the mentioned
Answer: a
Explanation: Watt’s governor is a pendulum type governor.
33. For isochronouns, spring controlled governor, the controlling force with increase in radius of rotation…….
A.increase
B.decreases
C.remains constant
D.behaves in unpredictable way
E.may increase or decrease depending on size
Answer: C
34. If the controlling force line for a spring controlled governor when produced intersects the y-axis at the origin, then governor is said to be…….
A.stable
B.unstable
C.isochronouns
D.sensitive
E.powerful
Answer: C
35. For a machine to be self-locking,its efficiency should be…….
A.100%
B.less than 67%
C.less than 50%
D.more than 50%
E.none of the above
Answer: C
36. Hartnell governor couldbe classified under the head of…….
A.inertia type governors
B.pendulum type governors
C.centrifugal type governors
D.dead weight type governors
E.none of the above
Answer: C.
37.. The governor used in gramophone is of the following type…….
A.Pickening
B.porter
C.hartnell
D.watt
E.hartung
Answer: A
1) Calculate the thrust in connecting rod, if piston effort is 200 kN and crank makes an angle of 45o from TDC. Assume obliquity ratio = 3.5
a. 900.80 kN
b. 204.20 kN
c. 195.87 kN
d. 970.02 kN
ANSWER: 204.20 kN
2) In the bifilar suspension system shown below if x = y, periodic oscillation tp is given as
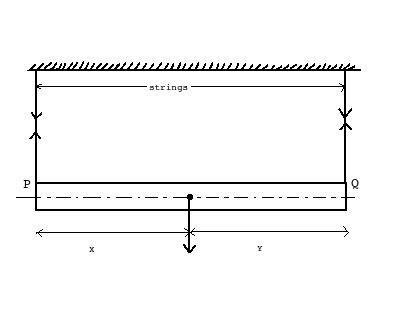
a. (2πk / x2) √(l / g)
b. (2πk / xy) √(l / g)
c. (2πk) √(l / gxy)
d. (2πk / x) √(l / g)
ANSWER: (2πk / x) √(l / g)
3) The difference between which two factors denotes the correction couple?
a. Difference between force required to accelerate non dynamically equivalent system and dynamically equivalent system
b. Difference between torque required to accelerate non dynamically equivalent system and dynamically equivalent system
c. Difference between torque required to decelerate dynamically equivalent system and non dynamically equivalent system
d. none of the above
ANSWER: Difference between torque required to accelerate non dynamically equivalent system and dynamically equivalent system
4) Which of the following statements is/are true?
1. Static force analysis does not consider inertia forces along with static forces
2. The SI unit of mass moment of inertia is kg/m2
3. Mass moment of inertia of a thin disc about its diameter is given by (mr2) / 2
a. Only 1
b. Only 2
c. Only 3
d. All the above statements are true
ANSWER: Only 1
5) According to D’ Alembert’s principle, the body is in equilibrium position if
a. inertia force is applied in the direction opposite to the resultant force
b. inertia force is applied in the same direction of the resultant force
c. both a. and b.
d. none of the above
ANSWER: inertia force is applied in the direction opposite to the resultant force
6) What is the equivalent length of simple pendulum, when compound pendulum is converted into simple pendulum?
a. le = (k + l ) / l
b. le = l2 / (k2 + l2)
c. le = (k2 + l2) / l
d. none of the above
ANSWER: le = (k2 + l2) / l
7) A connecting rod has periodic time of 1.5 sec/cycle for one oscillation. Calculate radius of gyration, when centre of gravity is at a distance of 500 mm from the small end.
a. 0.1325 m
b. 0.1719 m
c. 0.0295 m
d. 0.555 m
ANSWER: 0.1719 m
8) Trifilar suspension system is used to determine mass moment of inertia of
a. disc
b. flywheel
c. both a. and b.
d. none of the above
ANSWER: both a. and b.
9) Which formula is used to calculate correction couple?
a. Tc = ml1 (l3 – l2) α
b. Tc = ml1 (l3 – l2) α2
c. Tc = ml1 (l3 + l2) α
d. none of the above
ANSWER: Tc = ml1 (l3 – l2) α
10) On which factors does law of friction depend?
a. Nature of material
b. Area of contact between surfaces
c. Velocity of sliding
d. All of the above
ANSWER: Nature of material
11.Crank effort is the net force applied at the crankpin______to the crank which gives the required turning moment on the crankshaft.
(A)parallel
(B)perpendicular
(C)at 450
(D)1350
Answer:B
12.In a dynamically equivalent system, a uniformly distributed mass is divided into ____point masses.
(A)two
(B)three
(C)four
(D)five
Answer:A
13.Any distributed mass can be replaced by two point masses to have the same dynamical properties if
(A)the sum of the two masses are equal to the total mass
(B)the combined center of mass coincides with that of the rod
(C)the moment of inertia of two point masses about perpendicular axis through their combined center of mass is equal to that of the rod
(D)all of the mentioned
Answer:D
14.In a slider crank mechanism, if q and b are the angles made by the crank and the connecting rod respectively with the line of stroke and v is the linear velocity of the crank pin, the velocity of the slider is given by
(A)$$v\;\cos\left[90^\circ-(\theta-\beta)\right]\;\cos\beta$$
(B)$$v\;\cos\left[90^\circ+(\theta-\beta)\right]\;\cos\beta$$
(C)$$v\;\cos\left[90^\circ-(\theta+\beta)\right]\;\sin\beta$$
(D)$$v\;\cos\left[90^\circ-(\theta+\beta)\right]\;\cos\beta$$
Answer:D
15.Which of the following is not the required condition for replacing a rigid body by a dynamically equivalent system of two masses?
(A)The sum of the two masses are equal to the total mass.
(B)The sum of the squares of two masses are equal to the square of the total mass.
(C)The combined center of mass coincides with that of the rod.
(D)The moment of inertia of two point masses about perpendicular axis through their combined center of mass is equal to that of the rod.
Answer:B
16. Which of the following is incorrect regarding inertia force?
a) Imaginary force
b) Acts upon a rigid body
c) Brings the body to equilibrium
d) Same direction as of accelerating force
Answer: d
Explanation: The inertia force is an imaginary force, which on acting upon a rigid body has a tendency to bring it in an equilibrium position. Numerically it is equal to the magnitude of accelerating force, but the direction of this force is opposite.
17. Inertia torque acts in the same direction as the accelerating couple?
a) True
b) False
Answer: b
Explanation: The inertia torque is an imaginary torque, which when applied upon the rigid body, brings it in equilibrium position. It is equal to the accelerating couple in magnitude but opposite in direction.
18. If a force has a line of action at a distance h from the centre of gravity, then the value of h is given by _____
a) I. α/F
b) I. α/m.g
c) I/m.k
d) m.k/I
Answer: a
Explanation: We know that Force, F = Mass × Acceleration = m.a. and F.h = m.K2.α = I.α
Therefore, h = I. α/F.
19. D-Alembert’s principle is used for which of the following?
a) Change static problem into a dynamic problem
b) Change dynamic problem to static problem
c) To calculate moment of inertia of rigid bodies
d) To calculate angular momentum of a system of masses
Answer: b
Explanation: D-Alembert’s principle states that the resultant force acting on a body together with the reversed effective force (or inertia force), are in equilibrium. This principle is used to reduce a dynamic problem into an equivalent static problem.
20. In the expression F – m.a = 0, the term – m.a is called _______
a) Reversed effective force
b) Net force
c) Coriolis force
d) Resultant force
Answer: a
Explanation: If the quantity m.a is treated as another force with same line of action as the net force, then the body could be assumed to be in static equilibrium. This force is known as Reversed effective force.
21. Why the inertia torque acts in the opposite direction to the accelerating couple?
a) Bring the body in equilibrium
b) To reduce the accelerating torque
c) Acts as a constraint torque
d) Increase the linear acceleration
Answer: a
Explanation: The inertia torque is an imaginary torque, which when applied upon the rigid body, brings it in equilibrium position. It is equal to the accelerating couple in magnitude but opposite in direction.
22. A body remains in equilibrium if ________
a) Inertia force is applied in the same direction to the resultant force
b) Inertia force is applied in the direction opposite to the resultant force
c) Inertia force is applied in the direction Perpendicular to the resultant force
d) Inertia force is applied in the direction Parallel to the resultant force
Answer: b
Explanation: Inertia force is an imaginary force which tends to act in the direction opposite to the resultant force to bring the body in equilibrium. Numerically it is equal to the magnitude of accelerating force.
23. Inertia force and the reversed effective force are the same.
a) True
b) False
Answer: a
Explanation: The net force m.a is taken as another force acting in the opposite direction to the applied resultant force and is known as inertia force or reversed effective force.
24. In the following picture the G is the center of gravity, the quantity h is known as the “offset”. I is the moment of inertia and k is the radius of gyration. Offset’s value is given by?
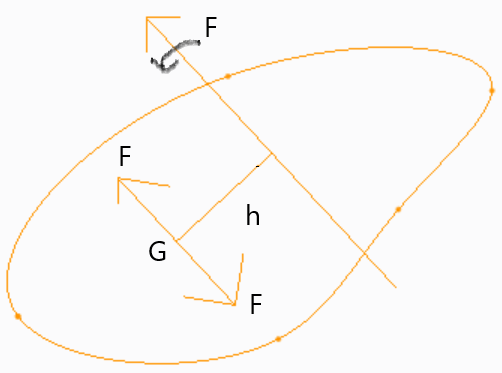
a) I.α/F
b) I.α/m.g
c) I/m.k
d) m.k/I
Answer: a
Explanation: We know that Force, F = Mass × Acceleration = m.a. and F.h = m.k2.α = I.α
Therefore, h = I.α/F
25. Considering a four bar chain with each link having linear and angular acceleration, applying D-Alembert’s principle will never result in which of the following member?
a) 2- force member
b) 3- force member
c) 4 – force member
d) Non accelerating member
Answer: a
Explanation: Since every link is accelerating it will have inertial torque and inertial force and at least force exerted by a link, thus it can never be a two force member.
26. Correction couple is applied when masses are placed arbitrarily and to maintain _________
a) Static equilibrium
b) Dynamic equilibrium
c) Stable equilibrium
d) Unstable equilibrium
Answer: b
Explanation: Difference between the torques required to accelerate the two-mass system and the torque required to accelerate the rigid body is called correction couple and this couple must be applied, when the masses are placed arbitrarily to make the system dynamical equivalent.
27. The sum of torques required to accelerate a 2 mass system and to accelerate a rigid body is called correction couple.
a) True
b) False
Answer: b
Explanation: Difference between the torques required to accelerate the two-mass system and the torque required to accelerate the rigid body is called correction couple.
28. The correction couple does not depend on _________
a) Distance between arbitrary masses
b) Distance between the two masses for a true dynamically equivalent system
c) Radius of gyration of equivalent system
d) Distance between fixed masses
Answer: d
Explanation: Distance between arbitrary masses, Distance between the two masses for a true dynamically equivalent system and Radius of gyration of equivalent system all effect the correction couple.
29. In the figure given below, A and D are arbitrary masses placed Quantity L is known as _______
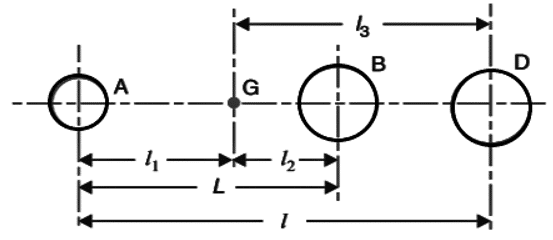
a) Distance between the two masses for a true dynamically equivalent system
b) Distance between fixed masses
c) Distance between arbitrary masses
d) Equivalent radius
Answer: a
Explanation: The distance between the two masses for a true dynamically equivalent system is given by L and has the expression of (Kg2 + l12)/l1.
30. An Internal combustion engine has a connecting rod of mass 2 kg and the distance between the centre of crank and centre of gudgeon pin is 25 cm. The Center of Gravity lies at a point 10 cm from the gudgeon pin along the line of centres. The radius of gyration of this system about an axis through the Center of Gravity perpendicular to the plane of rotation is 11 cm. Find the mass located at gudgeon pin in Kg.
a) 0.9
b) 0.8
c) 1.1
d) 1.2
Answer: c
Explanation: From the given data l = 25 cm, l1 = 10cm kg=11cm
l1.l2=kg2, l2 = 12.1 cm
M= l2m/( l1+ l2)
= 12.1x 2/( 12.1 + 10)
= 1.1 Kg.
31. From the data given:
54tr xc
Connecting rod of mass 2 kg and the distance between the centre of crank and centre of gudgeon pin is 25 cm. The Center of Gravity lies at a point 10 cm from the gudgeon pin along the line of centres.
The radius of gyration of this system about an axis through the Center of Gravity perpendicular to the plane of rotation is 11 cm.
Find the mass placed at distance l2 from center of gravity.
a) 0.9
b) 0.8
c) 1.1
d) 1.2
Answer: a
Explanation: From the given data l = 25 cm, l1 = 10cm kg=11cm
l1.l2=kg2, l2 = 12.1 cm
M = l1.m/( l1+ l2)
= 10×2(10+12.1)
= 0.9 kg.
32. An Internal combustion engine has a connecting rod of mass 2 kg and the distance between the centre of crank and centre of gudgeon pin is 25 cm. The Center of Gravity lies at a point 10 cm from the gudgeon pin along the line of centres. The radius of gyration of this system about an axis through the Center of Gravity perpendicular to the plane of rotation is 11 cm. If two masses are used instead of the connecting rod, one at the gudgeon pin and other at the crank pin. What will be the new radius of gyration?
a) 0.212m
b) 0.122m
c) 0.1m
d) 0.145m
Answer: b
Explanation: Let l3 be the distance between the masses, then l3 = l- l1 = 15cm
If K1 is the new radius of gyration then, K12= l1. l3 = 0.1×0.15 = 0.015 m2
Therefore, K1 = 0.122 m.
33. Mass moment of inertia of two arbitrary masses placed will be same as the mass moment inertia of the rigid body.
a) True
b) False
Answer: b
Explanation: Mass moment of inertia of two arbitrary masses placed will be different as the mass moment inertia of the rigid body, this is why there is a need to calculate the correction couple.
34. An Internal combustion engine has a connecting rod of mass 2 kg and the distance between the centre of crank and centre of gudgeon pin is 25 cm. The Center of Gravity lies at a point 10 cm from the gudgeon pin along the line of centres. The radius of gyration of this system about an axis through the Center of Gravity perpendicular to the plane of rotation is 11 cm. If two masses are used instead of the connecting rod, one at the gudgeon pin and other at the crank pin, if the angular acceleration of the rod is 23 000 rad/s2, then find the correction couple in N-m.
a) 140.2
b) 133.4
c) 136.8
d) 135.6
Answer: b
Explanation: We know that correction couple is given by T’ = m.(k12 – kg2).α
T’ = 2. (0.015 – 0.112). 23000
= 133.4 N-m.
1.When a rigid body is suspended vertically and it oscillates with a small amplitude under the action of the force of gravity, the body is known as
(A) simple pendulum
(B) torsional pendulum
(C) compound pendulum
(D) second’s pendulum
Answer:C
2.The time interval after which the motion is repeated itself is known as ___________ .
(A) time period
(B) cycle
(C) frequency
(D) isolation
Answer:A
3.Frequency of vibrations is usually expressed in
(A) number of cycles per hour
(B) number of cycles per minute
(C) number of cycles per second
(D) None of these
Answer:C
4.What is the effect on the undamped natural frequency of a single-degree-of-freedom system if the mass of the system is increased?
(A) The frequency will increase
(B) The frequency will stay the same
(C) The frequency will decrease
(D) None of these
Answer:C
5.The motion completed during one time period is known as _______.
(A) period of vibration
(B) cycle
(C) frequency
(D) all of the above
Answer:B
6. When there is a reduction in amplitude over every cycle of vibration, then the body is said to have
a) free vibration
b) forced vibration
c) damped vibration
d) none of the mentioned
Answer: c
Explanation: When no external force acts on the body, after giving it an initial displacement, then the body is said to be under free or natural vibrations. The frequency of the free vibrations is called free or natural frequency.
When there is a reduction in amplitude over every cycle of vibration, the motion is said to be damped vibration.
7. Longitudinal vibrations are said to occur when the particles of a body moves
a) perpendicular to its axis
b) parallel to its axis
c) in a circle about its axis
d) none of the mentioned
Answer: b
Explanation: When the particles of the shaft or disc moves parallel to the axis of the shaft, then the vibrations are known as longitudinal vibrations.
When the particles of the shaft or disc move approximately perpendicular to the axis of the shaft, then the vibrations are known as transverse vibrations.
8. When a body is subjected to transverse vibrations, the stress induced in a body will be
a) shear stress
b) tensile stress
c) compressive stress
d) none of the mentioned
Answer: b
Explanation: In transverse vibrations,the shaft is straight and bent alternately and bending stresses are induced in the shaft.
9. The natural frequency (in Hz) of free longitudinal vibrations is equal to
a) 1/2π√s/m
b) 1/2π√g/δ
c) 0.4985/δ
d) all of the mentioned
Answer: d
Explanation: Natural Frequency, fn = 0.4985/δ
where m = Mass of the body in kg,
s = Stiffness of the body in N/m, and
δ = Static deflection of the body in metres.
10. The factor which affects the critical speed of a shaft is
a) diameter of the disc
b) span of the shaft
c) eccentricity
d) all of the mentioned
Answer: d
Explanation: To determine the critical speed of a shaft which may be subjected to point loads, uniformly distributed load or combination of both, we find the frequency of transverse vibration which is equal to critical speed of a shaft in r.p.s. The Dunkerley’s method may be used for calculating the frequency.
11. The equation of motion for a vibrating system with viscous damping is
d2x/dt2 + c/m X dx/dt + s/m X x = 0
If the roots of this equation are real, then the system will be
a) over damped
b) under damped
c) critically damped
d) none of the mentioned
Answer: a
Explanation: When the roots are real, overdamping takes place.
When the roots are complex conjugate underdamping takes place.
12. In under damped vibrating system, if x1 and x2 are the successive values of the amplitude on the same side of the mean position, then the logarithmic decrement is equal to
a) x1/x2
b) log (x1/x2)
c) loge (x1/x2)
d) log (x1.x2)
Answer: b
Explanation: None
13. The ratio of the maximum displacement of the forced vibration to the deflection due to the static force, is known as
a) damping factor
b) damping coefficient
c) logarithmic decrement
d) magnification factor
Answer: d
Explanation: Magnificiant Factor is the ratio of maximum displacement of the forced vibration (xmax) to the deflection due to the static force F(xo).
Damping Factor is the ratio of amping coefficient for the actual system, and damping coefficient for the critical damped system.
14. In vibration isolation system, if ω/ωn is less than √2 , then for all values of the damping factor, the transmissibility will be
a) less than unity
b) equal to unity
c) greater than unity
d) zero
where ω = Circular frequency of the system in rad/s, and
ωn = Natural circular frequency of vibration of the system in rad/s.
Answer: c
Explanation: The value of ω/ωn must be greater than √2 if ε is to be less than 1 and it is the numerical value of ε , independent of any phase difference between the forces that may exist which is important.
15. In vibration isolation system, if ω/ωn > 1, then the phase difference between the transmitted force and the disturbing force is
a) 0°
b) 90°
c) 180°
d) 270°
Answer: c
Explanation: There is a phase difference of 180° between the transmitted force and the disturbing force.
16) Calculate logarithmic decrement if damping factor is 0.33.
a. 1.36
b. 3.23
c. 5.16
d. 2.19
ANSWER: 2.19
17) Calculate coefficient of viscous damper, if the system is critically damped.
Consider the following data:
1. Mass of spring mass damper system = 350 kg
2. Static deflection = 2 x 10–3 m
3. Natural frequency of the system = 60 rad/sec
a. 100.5 x 103 N-s/m
b. 80 x 103 N-s/m
c. 42 x 103 N-s/m
d. None of the above
ANSWER: 42 x 103 N-s/m
18) Determine logarithmic decrement, if the amplitude of a vibrating body reduces to 1/6th in two cycles.
a. 0.223
b. 0.8958
c. 0.3890
d. None of the above
ANSWER: 0.8958
19) Determine natural frequency of a system, which has equivalent spring stiffness of 30000 N/m and mass of 20 kg?
a. 12.32 Hz
b. 4.10 Hz
c. 6.16 Hz
d. None of the above
ANSWER: 6.16 Hz
20) Calculate natural frequency of damped vibration, if damping factor is 0.52 and natural frequency of the system is 30 rad/sec which consists of machine supported on springs and dashpots.
a. 25.62 rad/sec
b. 20.78 rad/sec
c. 14.4 rad/sec
d. 15.33 rad/sec
ANSWER: 25.62 rad/sec
21) In damped free vibrations, which parameters indicate vibrations?
a. Natural frequency
b. Rate of decay of amplitude
c. Both a. and b.
d. None of the above
ANSWER: Both a. and b.
22) According to D’ Alembert’s principle, m (d2x/ dt2) + c (dx/dt) + Kx =0 is the differential equation for damped free vibrations having single degree of freedom. What will be the solution to this differential equation if the system is critically damped?
a. x = (A + Bt) e– ωt
b. x = X e– ξωt (sin ωdt + Φ)
c. x = (A – Bt) e– ωt
d. x = X e– ξωt (cos ωdt + Φ)
ANSWER: x = (A + Bt) e– ωt
23) Which of the following statements is/are true for coulomb damping?
1. Coulomb damping occurs due to friction between two lubricated surfaces
2. Damping force is opposite to the direction of motion of vibrating body
3. For smooth surfaces, coefficient of friction depends upon velocity
4. Damping force depends upon the rubbing velocity between two rubbing surfaces
a. Only statement 1
b. Statement 2, 3 and statement 4
c. Only statement 2
d. All the above statements are true
ANSWER: Only statement 2
24) What is meant by critical damping coefficient?
a. Frequency of damped free vibrations is less than zero
b. The motion is aperiodic in nature
c. Both a. and b.
d. None of the above
ANSWER: The motion is aperiodic in nature
25) Which of the following relations is true for viscous damping?
a. Force α relative displacement
b. Force α relative velocity
c. Force α (1 / relative velocity)
d. None of the above
ANSWER: Force α relative velocity
26. Fluid resistance causes damping which is known as ______
a) Resistance damping
b) Fluid damping
c) Viscous damping
d) Liquid damping
Answer: c
Explanation: Damping due to the resistance offered by the fluid is known as viscous damping. This is because of the reduction in the amplitude caused by the viscous forces of the fuild.
27. In damped vibrations, the amplitude of the resulting vibration gradually diminishes.
a) True
b) False
Answer: a
Explanation: Since a certain amount of energy is always dissipated while overcoming the resistance forces, In damped vibrations, the amplitude of the resulting vibration gradually diminishes.
28. In damped vibrations, the amplitude of the resulting vibration gradually reduces. This is due to the reason that an amount of energy is always dissipated to overcome the ________
a) Frictional resistance
b) Work done
c) Fluid pressure
d) Air pressure
Answer: a
Explanation: In case of damped vibrations, the amplitude of the resulting vibration gradually diminishes. This is due to the reason that a certain amount of energy is always dissipated to overcome the frictional resistance.
29. The resistance to the motion of the body is provided by ______
a) Medium of vibration
b) Speed of vibration
c) Length of the material
d) External friction
Answer: a
Explanation: The resistance to the motion of the vibrating body is provided partly by the medium in which the vibration takes place and partly by the internal friction.
30. In which direction does the damping force acts?
a) Opposite to the motion
b) Along the motion
c) Perpendicular to motion
d) Variable
Answer: a
Explanation: It is assumed that the frictional resistance to the motion of the body is directly proportional to the speed of, therefore Damping force or frictional force on the mass acts in opposite direction to the motion of the mass.
31. In which direction does the accelerating force acts?
a) Opposite to the motion
b) Along the motion
c) Perpendicular to motion
d) Variable
Answer: b
Explanation: It is assumed that the frictional resistance to the motion of the body is directly proportional to the speed, therefore accelerating force on the mass acts in same direction to the motion of the mass.
32. In which of the following cases, overdamping occurs?
a) Roots are real
b) Roots are complex conjugate
c) Roots are equal
d) Independent of the equation
Answer: a
Explanation: If the roots k1 and k2 are real but negative the case is of overdamping or large damping and the mass moves slowly to the equilibrium position. This motion is known as aperiodic.
33. In which of the following cases, underdamping occurs?
a) Roots are real
b) Roots are complex conjugate
c) Roots are equal
d) Independent of the equation
Answer: b
Explanation: If the roots k1 and k2 are complex, the case is of underdamping or small damping and the mass moves slowly to the equilibrium position.
1. Fluid resistance causes damping which is known as ______
a) Resistance damping
b) Fluid damping
c) Viscous damping
d) Liquid damping
Answer: c
Explanation: Damping due to the resistance offered by the fluid is known as viscous damping. This is because of the reduction in the amplitude caused by the viscous forces of the fuild.
2. In damped vibrations, the amplitude of the resulting vibration gradually diminishes.
a) True
b) False
Answer: a
Explanation: Since a certain amount of energy is always dissipated while overcoming the resistance forces, In damped vibrations, the amplitude of the resulting vibration gradually diminishes.
3. In damped vibrations, the amplitude of the resulting vibration gradually reduces. This is due to the reason that an amount of energy is always dissipated to overcome the ________
a) Frictional resistance
b) Work done
c) Fluid pressure
d) Air pressure
Answer: a
Explanation: In case of damped vibrations, the amplitude of the resulting vibration gradually diminishes. This is due to the reason that a certain amount of energy is always dissipated to overcome the frictional resistance.
4. The resistance to the motion of the body is provided by ______
a) Medium of vibration
b) Speed of vibration
c) Length of the material
d) External friction
Answer: a
Explanation: The resistance to the motion of the vibrating body is provided partly by the medium in which the vibration takes place and partly by the internal friction.
5. In which direction does the damping force acts?
a) Opposite to the motion
b) Along the motion
c) Perpendicular to motion
d) Variable
Answer: a
Explanation: It is assumed that the frictional resistance to the motion of the body is directly proportional to the speed of, therefore Damping force or frictional force on the mass acts in opposite direction to the motion of the mass.
6. In which direction does the accelerating force acts?
a) Opposite to the motion
b) Along the motion
c) Perpendicular to motion
d) Variable
Answer: b
Explanation: It is assumed that the frictional resistance to the motion of the body is directly proportional to the speed, therefore accelerating force on the mass acts in same direction to the motion of the mass.
7. In which of the following cases, overdamping occurs?
a) Roots are real
b) Roots are complex conjugate
c) Roots are equal
d) Independent of the equation
Answer: a
Explanation: If the roots k1 and k2 are real but negative the case is of overdamping or large damping and the mass moves slowly to the equilibrium position. This motion is known as aperiodic.
8. In which of the following cases, underdamping occurs?
a) Roots are real
b) Roots are complex conjugate
c) Roots are equal
d) Independent of the equation
Answer: b
Explanation: If the roots k1 and k2 are complex, the case is of underdamping or small damping and the mass moves slowly to the equilibrium position.
9) Calculate damped natural frequency, if a spring mass damper system is subjected to periodic disturbing force of 30 N. Damping coefficient is equal to 0.76 times of critical damping coefficient and undamped natural frequency is 5 rad/sec
a. 3.99 rad/sec
b. 2.13 rad/sec
c. 4.12 rad/sec
d. 3.24 rad/sec
ANSWER: 3.24 rad/sec
10) Calculate critical speed of a vehicle which moves on a road having sinusoidal profile of wavelength 2.5 m. The mass of the vehicle is 300 kg and natural frequency of its spring suspension system is 8 rad/sec
a. 4.15 m/sec
b. 3.18 m/sec
c. 2.36 m/sec
d. None of the above
ANSWER: 3.18 m/sec
11) What is the effect of damping on phase angle at resonance frequency?
a. Phase angle increases as damping increases
b. Damping has no effect on phase angle
c. Phase angle increases as damping decreases
d. None of the above
ANSWER: Damping has no effect on phase angle
12) When frequency ratio (ω/ωn) is greater than unity, phase angle decreases as ______
a. damping factor increases
b. damping factor decreases
c. both a. and b.
d. none of the above
ANSWER: damping factor increases
13) At which frequency ratio, phase angle increases as damping factor increases?
a. When frequency ratio is less than unity
b. When frequency ratio is more than unity
c. When frequency ratio is zero
d. All of the above
ANSWER: When frequency ratio is less than unity
14) Which of the following statements is/are true?
1. Magnification factor is minimum at resonance
2. The maximum value of amplification factor increases as damping factor decreases
3. The maximum value of amplification factor increases as damping factor increases
4. Magnification factor is maximum at resonance
a. Statement 1 and statement 2
b. Statements 1,2 and 3
c. Statement 2 and statement 4
d. All the above statements are true
ANSWER: Statement 2 and statement 4
15) Magnification factor is the ratio of ______
a. zero frequency deflection and amplitude of steady state vibrations
b. amplitude of steady state vibrations and zero frequency deflection
c. amplitude of unsteady state vibrations and zero frequency distribution
d. none of the above
ANSWER: amplitude of steady state vibrations and zero frequency deflection
16) Consider the steady-state absolute amplitude equation shown below, if ω / ωn = √2 then amplitude ratio (X/Y) =?
(X/Y) = √{1 + [ 2ξ (ω/ωn)]2} / √{[1 – (ω/ωn)2]2 + {2ξ (ω/ωn)2}
a. 0
b. 1
c. less than 1
d. greater than 1
ANSWER: 1
17) What is meant by phase difference or phase angle in forced vibrations?
a. Difference between displacement vector (xp) and velocity vector Vp
b. Angle in which displacement vector leads force vector by (F0 sinωt)
c. Angle in which displacement vector (xp) lags force vector (F0 sinωt)
d. None of the above
ANSWER: Angle in which displacement vector (xp) lags force vector (F0 sinωt)
18) The equation m(d2x/ dt2) + c (dx/dt) + Kx = F0 sin ωt is a second order differential equation. The solution of this linear equation is given as
a. complementary function
b. particular function
c. sum of complementary and particular function
d. difference of complementary and particular function
ANSWER: sum of complementary and particular function
19) Calculate damped natural frequency, if a spring mass damper system is subjected to periodic disturbing force of 30 N. Damping coefficient is equal to 0.76 times of critical damping coefficient and undamped natural frequency is 5 rad/sec
a. 3.99 rad/sec
b. 2.13 rad/sec
c. 4.12 rad/sec
d. 3.24 rad/sec
ANSWER: 3.24 rad/sec
20. A single degree of freedom system is given by, m × (d²x/dt²) + c × (dx/dt) + sx = F.cosω.t with usual notations. It represents
(A) Free vibration with damping
(B) Free vibration without damping
(C) Forced vibration with damping
(D) Forced vibration without damping
Answer:c
21. The factional torque for square thread at the mean radius r while raising load W is given by
(A) T = W.r tan(φ – α)
(B) T = W.r tan(φ + α)
(C) T = W.r tanα
(D) T = W.r tanφ
Answer:b
22. In a band and block brake, the ratio of tensions on tight side and slack side of the band is (where μ = Coefficient of friction between the blocks and the drum, θ = Semi-angle of each block subtending at the center of drum, and n = Number of blocks)
(A) T₁/T₂ = μ. θ. n
(B) T₁/T₂ = [(1 – μ tanθ)/(1 + μ tanθ)]n
(C) T₁/T₂ = (μ θ)n
(D) T₁/T₂ = [(1 + μ tanθ)/(1 – μ tanθ)]n
Answer:d
23. An involute pinion and gear are in mesh. If both have the same size of addendum, then there will be an interference between the
(A) Tip of the gear tooth and flank of pinion
(B) Tip of the pinion and flank of gear
(C) Flanks of both gear and pinion
(D) Tip of both gear and pinion
Answer:a
24. A universal joint is an example of
(A) Higher pair
(B) Lower pair
(C) Rolling pair
(D) Sliding pair
Answer:b
25. Oldham’s coupling is the
(A) Second inversion of double slider crank chain
(B) Third inversion of double slider crank chain
(C) Second inversion of single slider crank chain
(D) Third inversion of slider crank chain
Answer:b
26. Transmission of power from the engine to the rear axle of an automobile is by means of
(A) Compound gears
(B) Worm and wheel method
(C) Hooke’s joint
(D) Crown gear
Answer:c
27. Which of the following property of the instantaneous center is correct?
(A) A rigid link rotates instantaneously relative to another link at the instantaneous centre for the configuration of the mechanism considered.
(B) The two rigid links have no linear velocity relative to each other at the instantaneous centre.
(C) The velocity of the instantaneous centre relative to any third rigid link is same whether the instantaneous centre is regarded as a point on the first rigid link or on the second rigid link.
(D) All of the above
Answer:d
28. When the addenda on pinion and wheel is such that the path of approach and path of recess are half of their maximum possible values, then the length of the path of contact is given by (where r = Pitch circle radius of pinion, R = Pitch circle radius of wheel, and φ = Pressure angle)
(A) [(r² + R²) cosφ]/2
(B) [(r² + R²) sinφ]/2
(C) [(r + R) cosφ]/2
(D) [(r + R) sinφ]/2
Answer:d
29. A rotor which is balanced statically but not dynamically is supported on two bearings L apart and at high speed of the rotor, reaction on the left bearing is R. The right side of the bearing is shifted to a new position 2L apart from the left bearing. At the same rotor speed, dynamic reaction on the left bearing in the new arrangement will
(A) Remain same as before
(B) Become equal to 2R
(C) Become equal to R/2
(D) Become equal to R/4
Answer:a
30. To transmit power from one rotating shaft to another whose axes are neither parallel nor intersecting, use?
(A) Spur gear
(B) Spiral gear
(C) Bevel gear
(D) Worm gear
Answer:d
31. Hart mechanism has
(A) Eight links
(B) Six links
(C) Four links
(D) Twelve links
Answer:b
32. The dedendum circle diameter is equal to (where, φ = Pressure angle)
(A) Pitch circle dia. × cosφ
(B) Addendum circle dia. × cosφ
(C) Clearance circle dia. × cosφ
(D) Pitch circle dia. × sinφ
Answer:a
33. The acceleration of a particle moving with simple harmonic motion, at any instant is given by
(A) ωx
(B) ω²x
(C) ω²/x
(D) ω³/x
Answer:b
34. The equation of motion for a vibrating system with viscous damping is
(d²x/dt²) + (c/m). (dx/dt) + (s/m). x = 0
If the roots of this equation are real, then the system will be
(A) Over-damped
(B) Under damped
(C) Critically damped
(D) Without vibrations
Answer:a
1) Calculate damped natural frequency, if a spring mass damper system is subjected to periodic disturbing force of 30 N. Damping coefficient is equal to 0.76 times of critical damping coefficient and undamped natural frequency is 5 rad/sec
a. 3.99 rad/sec
b. 2.13 rad/sec
c. 4.12 rad/sec
d. 3.24 rad/sec
ANSWER: 3.24 rad/sec
2) Calculate critical speed of a vehicle which moves on a road having sinusoidal profile of wavelength 2.5 m. The mass of the vehicle is 300 kg and natural frequency of its spring suspension system is 8 rad/sec
a. 4.15 m/sec
b. 3.18 m/sec
c. 2.36 m/sec
d. None of the above
ANSWER: 3.18 m/sec
3) What is the effect of damping on phase angle at resonance frequency?
a. Phase angle increases as damping increases
b. Damping has no effect on phase angle
c. Phase angle increases as damping decreases
d. None of the above
ANSWER: Damping has no effect on phase angle
4) When frequency ratio (ω/ωn) is greater than unity, phase angle decreases as ______
a. damping factor increases
b. damping factor decreases
c. both a. and b.
d. none of the above
ANSWER: damping factor increases
5) At which frequency ratio, phase angle increases as damping factor increases?
a. When frequency ratio is less than unity
b. When frequency ratio is more than unity
c. When frequency ratio is zero
d. All of the above
ANSWER: When frequency ratio is less than unity
6) Which of the following statements is/are true?
1. Magnification factor is minimum at resonance
2. The maximum value of amplification factor increases as damping factor decreases
3. The maximum value of amplification factor increases as damping factor increases
4. Magnification factor is maximum at resonance
a. Statement 1 and statement 2
b. Statements 1,2 and 3
c. Statement 2 and statement 4
d. All the above statements are true
ANSWER: Statement 2 and statement 4
7) Magnification factor is the ratio of ______
a. zero frequency deflection and amplitude of steady state vibrations
b. amplitude of steady state vibrations and zero frequency deflection
c. amplitude of unsteady state vibrations and zero frequency distribution
d. none of the above
ANSWER: amplitude of steady state vibrations and zero frequency deflection
8) Consider the steady-state absolute amplitude equation shown below, if ω / ωn = √2 then amplitude ratio (X/Y) =?
(X/Y) = √{1 + [ 2ξ (ω/ωn)]2} / √{[1 – (ω/ωn)2]2 + {2ξ (ω/ωn)2}
a. 0
b. 1
c. less than 1
d. greater than 1
ANSWER: 1
9) What is meant by phase difference or phase angle in forced vibrations?
a. Difference between displacement vector (xp) and velocity vector Vp
b. Angle in which displacement vector leads force vector by (F0 sinωt)
c. Angle in which displacement vector (xp) lags force vector (F0 sinωt)
d. None of the above
ANSWER: Angle in which displacement vector (xp) lags force vector (F0 sinωt)
10) The equation m(d2x/ dt2) + c (dx/dt) + Kx = F0 sin ωt is a second order differential equation. The solution of this linear equation is given as
a. complementary function
b. particular function
c. sum of complementary and particular function
d. difference of complementary and particular function
ANSWER: sum of complementary and particular function
11. Which of the following systems produce a vibration in the foundation?
a) Unbalanced machine
b) Balanced machine
c) Coupled machine
d) Uncoupled machine
Answer: a
Explanation: It has been observed that when an unbalanced machine is installed on the foundation, it produces vibration in the foundation which needs to be countered to create smooth working of the machine.
12. When a periodic disturbing force is applied to a machine, the force is transmitted to the foundation by the means of spring.
a) True
b) False
Answer: a
Explanation: Springs or dampers are mounted on the machine in order to reduce the vibrations produce but however they also transmit the disturbing periodic force to the machine.
13. Which of the following is correct regarding isolation factor?
a) Dimensionless quantity
b) Has Newton as its unit
c) Has joule as its Unit
d) Has Hz as its unit
Answer: a
Explanation: Isolation factor is a ratio of transmitted force to the applied force, since it is a ratio of two quantities having same dimension, it is a dimensionless quantity.
14. Which of the following is a type of transmitted force to the foundation?
a) Damping force
b) Undamping force
c) Tensile force
d) Torsional force
Answer: a
Explanation: The transmitted force consists of the following two forces which are perpendicular to each other namely: Spring or elastic force and damping force. This happens as both spring and damper is used in order to minimize vibrations.
15. If the damper is not provided and the system is in resonance, which of the following is the correct isolation factor?
a) 0
b) 1/2
c) 1/4
d) Infinity
Answer: d
Explanation: When the damper is not involved, the damping coefficient c becomes zero and isolation factor is given by:
1/(1-(ω/ωn))
Since during resonance, ω=ωn
isolation factor becomes infinite.
16. If isolation factor is negative, then what is the phase difference between transmitted and disturbing force?
a) 180°
b) 90°
c) 450°
d) 360°
Answer: a
Explanation: If the isolation factor is negative then the ratio ω/ωn is greater than 1, in this case the phase difference between the disturbing force and the transmitted force is 180°.
17. Which of the following is true regarding Ɛ>1?
a) Transmitted force is greater than applied force
b) Transmitted force is less than applied force
c) Spring force is less than applied force
d) Damping force is less than applied force
Answer: a
Explanation: if the isolation factor is greater than 1, then the ratio ω/ωn < √2, this means that there is a phase difference between the transmitted force and the disturbing force, where the transmitted force is greater than the applied force.
18. Isolation factor is twice the transmissibility ratio.
a) True
b) False
Answer: b
Explanation: The given statement is false as the isolation factor and the transmissibility ratio have the same value which is given by ratio of Transmitted force to the Applied force.
19) A vibrating machine of 100 kg is mounted on a rubber pad which has stiffness of 500 N/m. Determine force transmitted to the foundation if the unbalanced force 500 N acts on it. The frequency ratio (ω/ωn) is 1.5 and ξ = 0.5
a. 461.62 N
b. 400.23 N
c. 450 N
d. Insufficient data
ANSWER: 461.62 N
20) Which of the following statements is/are false for pneumatic isolators ?
1. Pneumatic isolators are used when driving frequencies below 10 Hz are present
2. Nausea is caused due to noise at low frequencies
3. At high natural frequencies, isolators can obtain efficiency of 90%
4. Pneumatic isolators have limited load carrying capacity
a. Only statement 1
b. Only statement 3
c. Only statement 2, 4
d. All the above statements are false
ANSWER: Only statement 3
21) Which of the following statements is/are true for elastomers?
a. Elastomers can be used for static deflections up to 12 mm
b. Elastomers can provide natural frequencies below 5 Hz
c. Elastomers have good performance at high frequencies
d. All the above statements are true
ANSWER: All the above statements are true
22) Transmissibility is the ratio of ______
a. force transmitted to the supporting structure and force impressed upon the system
b. displacement amplitude of mass and displacement amplitude of supporting structure
c. both a. and b.
d. none of the above
ANSWER: both a. and b.
23) What is the function of the controller in active vibration isolation systems?
a. Detect vibrations to be controlled
b. Reposition the masses
c. Interpret detected vibrations and execute commands
d. All of the above
ANSWER: Interpret detected vibrations and execute commands
24) Which among the following is not considered when reference standards are used in the field of mechanical vibration and shock, monitoring and analysis of machines?
a. Terminology
b. Methods of testing
c. Methods of measurement
d. None of the above
ANSWER: None of the above
25) Which basic document describes general requirements for measurement and evaluation of machine vibrations using shaft measurements?
a. ISO – 10816-1
b. ISO – 7919-1
c. Both a. and b.
d. None of the above
ANSWER: ISO – 7919-1
26) In the graph shown below, the region in which frequency ratio (ω/ωn) > √2 is known as____
a. Amplification region
b. Isolation region
c. Spring controlled region
d. None of the above
ANSWER: Isolation region
27) Which of the following is a type of untuned vibration absorber?
a. Houdaille damper
b. Torsional vibration absorber
c. Centrifugal pendulum absorber
d. All of the above
ANSWER: Houdaille damper
29) Which of the following methods can be used to reduce excitation level at the source?
a. Lubrication of joints
b. Balancing inertia forces
c. Both a. and b.
d. None of the above
ANSWER: Both a. and b.
30. In gears, interference takes place when
(A) The tip of a tooth of a mating gear digs into the portion between base and root circles
(B) Gears do not move smoothly in the absence of lubrication
(C) Pitch of the gears is not same
(D) Gear teeth are undercut
Answer:a
31. In under damped vibrating system, the amplitude of vibration
(A) Decreases linearly with time
(B) Increases linearly with time
(C) Decreases exponentially with time
(D) Increases exponentially with time
Answer:c
32. A body is said to be under forced vibrations, when
(A) There is a reduction in amplitude after every cycle of vibration
(B) No external force acts on a body, after giving it an initial displacement
(C) A body vibrates under the influence of external force
(D) None of the above
Answer:a
33. Creep in belt drive is due to
(A) Weak material of the belt
(B) Weak material of the pulley
(C) Uneven extensions and contractions of the belt when it passes from tight side to slack side
(D) Expansion of the belt
Answer:a
34) Temperature monitoring technique uses which of the following devices to measure temperature of the machining surfaces?
a. Pyrometers
b. Thermocouples
c. Thermometers
d. All of the above
ANSWER: All of the above
35) Which of the following statements is true about stroboscope?
a. Stroboscope is non-contact type frequency instrument
b. Stroboscope can measure frequency upto 5 Hz
c. Stroboscope uses electromagnetic radiations to measure frequency
d. All of the above
ANSWER: Stroboscope is non-contact type frequency instrument
36) Which type of frequency measuring instrument has multiple reeds of different natural frequency to measure vibrations?
a. Fullarton tachometer
b. Frahm Tachometer
c. Both a. and b.
d. None of the above
ANSWER: Frahm Tachometer
37) Which type of instruments do not require separate power source for measuring vibratory response of a vibratory system?
a. Active instruments
b. Passive instruments
c. Both a. and b.
d. None of the above
ANSWER: Passive instruments
38) Which of the following instruments measure amplitude of a vibrating body?
a. Vibrometers
b. Seismometer
c. Both a. and b.
d. None of the above
ANSWER: Both a. and b.
39) Which of the following conditions is/are to be satisfied by the seismometer for it to be used as velometer?
a. It’s natural frequency should be large
b. It’s natural frequency should be small
c. It’s output signal should be proportional to relative acceleration of the vibrating body
d. None of the above
ANSWER: It’s natural frequency should be small
40) Which of the following vibrometers have frequency ratio (ω/ωn) << 1?
a. Accelerometers
b. Velometers
c. Both a. and b.
d. None of the above
ANSWER: Accelerometers
41) In graph of (Transmissibility vs Frequency Ratio) shown below, the shaded region is called as____
a. Spring controlled region
b. Damping controlled region
c. Mass controlled region
d. None of the above
ANSWER: Mass controlled region
42) Which type of monitoring system uses stroboscope to measure speed of the machine?
a. Portable condition monitoring system
b. Basic condition monitoring system
c. Computer based condition monitoring system
d. None of the above
ANSWER: Basic condition monitoring system
43) Seismometer can be used to measure acceleration of any instrument only if _____
a. it’s natural frequency is high
b. it generates output signal which is proportional to relative acceleration of the vibrating object
c. both a. and b.
d. none of the above
ANSWER: both a. and b.
1. Consider P and Q as the shaft having two rotors at the end of it, what is the point N known as in the given figure?
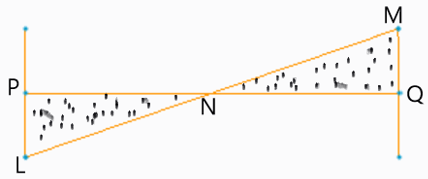
a) Node
b) Elastic point
c) Inelastic point
d) Breaking point
Answer: a
Explanation: The torsional vibrations occur in a two-rotor system only if the rotors move in the opposite direction, at point N there is no vibration hence it is known as node.
2. In a two rotor system, torsional vibration occurs only if the rotors are moving in the same direction.
a) True
b) False
Answer: b
Explanation: For a two rotor system, the torsional vibration will occur only if the rotors are moving in the direction opposite to each other.
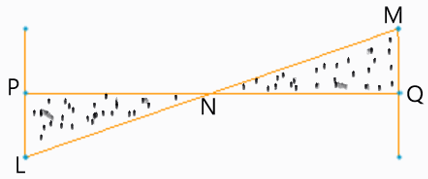
3. In the given figure representing a two rotor system, what is the line LNM called?
a) Node line
b) Elastic line
c) Inelastic line
d) Breaking line
Answer: b
Explanation: The given figure represents the shaft PQ with rotors attached to the end of it making it a two rotor system, in the figure, the line LNM is known as the elastic line of the shaft.
4. For occurrence of free torsional vibration which of the condition is necessary?
a) Rotors moving in same direction
b) Rotors having same frequency
c) Rotors having different frequency
d) Rotors rotate in the same sense
Answer: b
Explanation: In a two rotor torsional vibration system, the system will rotate if the rotors are rotating in opposite direction with the same frequency.
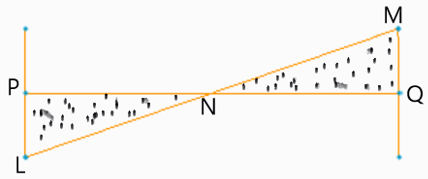
5. In the given figure, considering PN as one shaft, If the mass moment of inertia is increased to four times, then what will be the effect on free torsional vibrations of a rotor at P?
a) Increases 4 times
b) Increases 2 times
c) Decreases 4 times
d) Decreases 2 times
Answer: d
Explanation: If N is the node then PN can be considered as a shaft of single rotor system, since the free torsional vibrations of a single motor system depends on the inverse of square root of the mass moment of inertia of the system, increasing 4 times will lead to decrease in two times the initial vibration.
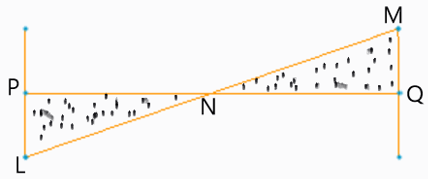
6. In the given figure if N is the node then NQ acts as which of the following system?
a) Single rotor system
b) Two rotor system
c) Three rotor system
d) Four rotor system
Answer: a
Explanation: If N is the node in the given figure, then N can act as a fixed end of the shaft NQ where the rotor is connected at Q, hence it acts like a single rotor system.
7. Keeping the mass moment of inertia of both the shafts in a two rotor system same, if the length of one shaft is doubled what should be the effect on the length of other shaft?
a) Doubled
b) Halved
c) Constant
d) Increased to 4 times
Answer: a
Explanation: The vibration will occur in a two rotor system only if the frequencies of both the rotors are same, hence L(a)I(a) = L(b)I(b). Therefore the relation is directly proportional.
8. For a two rotor system, the mass moment of inertia of one shaft(A) is twice the other(B), then what is the relation between the length of the shafts.
a) 2L(A) = L(B)
b) L(A) = 2L(B)
c) L(A) = L(B)
d) 2L(A) = 3L(B)
Answer: a
Explanation: For a two rotor system, we have L(A)I(A) = L(B)I(B)
Now I(A)=2I(B)
Therefore, 2L(A) = L(B).
9. For a two rotor system, the length of one shaft(A) is twice the other(B), then what is the relation between the Mass moment of inertia of the shafts.
a) 2I(A) = I(B)
b) I(A) = 2I(B)
c) I(A) = I(B)
d) 2I(A) = 3I(B)
Answer: a
Explanation: For a two rotor system, we have L(A)I(A) = L(B)I(B)
Now L(A)=2L(B)
Therefore, 2I(A) = I(B).
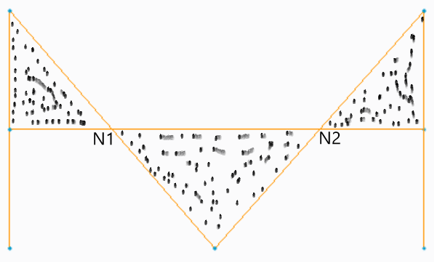
10. In the figure given below, the points N1 and N2 are known as_______
a) Nodes
b) Elastic points
c) Inelastic points
d) Breaking points
Answer: a
Explanation: The torsional vibrations occur in a three rotor system only if there are one node or two nodes, at points N1 and N2 there is no vibration hence they are known as nodes.
11. In a three rotor system, free torsional vibration cannot occur if there is only one node.
a) True
b) False
Answer: b
Explanation: In a three rotor system there may occur one or two nodes, free torsional vibration may occur in presence of either one or two nodes.
12. In which of the following condition torsional vibration will not take place, considering 3 rotors A, B and C. A is rotating in clockwise direction.
a) B in clockwise C in anticlockwise
b) C in clockwise B in anticlockwise
c) B and C in clockwise
d) B and C in anticlockwise
Answer: c
Explanation: For a three rotor system torsional vibration will occur only if two of the three rotors are rotating in the same direction and the third one is rotating in the opposite direction.
13. For occurrence of free torsional vibration in a three rotor system which of the condition is necessary?
a) Rotors moving in same direction
b) Rotors having same frequency
c) Rotors having different frequency
d) Rotors rotate in the same sense
Answer: b
Explanation: In a three rotor torsional vibration system, the system will rotate if the two rotors are rotating in same direction and the third one with opposite direction all with the same frequency.
14. the given figure, considering left end has one rotor, If the mass moment of inertia of the shaft till node N1 is increased to four times, then what will be the effect on free torsional vibrations of a rotor at left end of N1?
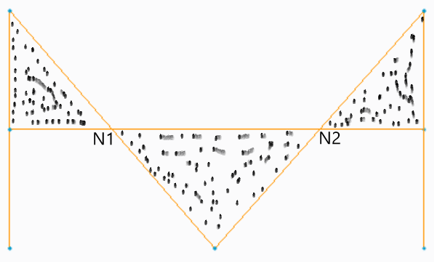
a) Increases 4 times
b) Increases 2 times
c) Decreases 4 times
d) Decreases 2 times
Answer: d
Explanation: If N1 is the node then left end and N1 can be considered as a shaft of single rotor system, since the free torsional vibrations of a single motor system depends on the inverse of square root of the mass moment of inertia of the system, increasing 4 times will lead to decrease in two times the initial vibration.
15. In the given figure if N1 is the node then N1Q acts as which of the following system?
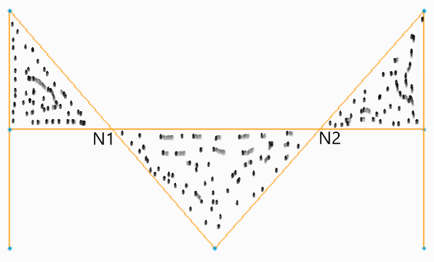
a) Single rotor system
b) Two rotor system
c) Three rotor system
d) Four rotor system
Answer: b
Explanation: If N1 is the node in the given figure, then N1 can act as a fixed end of the shaft N1N2 where the rotor is connected at Q and N1, hence it acts like a two rotor system.
16. Keeping the mass moment of inertia of left end and the right end shafts in a three rotor system same, if the length of one shaft is doubled what should be the effect on the length of other shaft?
a) Doubled
b) Halved
c) Constant
d) Increased to 4 times
Answer: a
Explanation: The vibration will occur in a two rotor system only if the frequencies of both the rotors are same, hence L(a)I(a) = L(c)I(c). Therefore the relation is directly proportional.
17. Free torsional vibrations will occur in a three rotor system only if all rotors have same frequency.
a) True
b) False
Answer: a
Explanation: In a three rotor system the free torsional vibration will occur only if all the rotors have the same frequency of vibration and two have common rotation sense.
18. What is the total number of nodes formed in a three rotor system if the rotors at one of the ends and the one in the middle rotate in the same direction?
a) 0
b) 1
c) 2
d) 3
Answer: b
Explanation: In a three rotor system, if the rotor at one of the ends and the one in the middle are rotating in the same direction, then there is formation of only one node.
19. For a three rotor system in the figure given below, the length of one shaft(P) is twice the other(Q), then what is the relation between the Mass moment of inertia of the shafts.
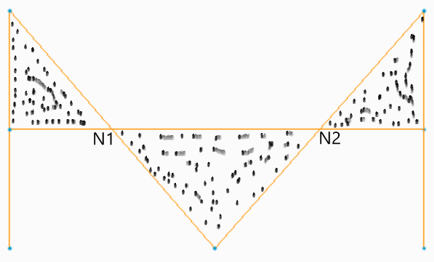
a) 2I(P) = I(Q)
b) I(P) = 2I(Q)
c) I(P) = I(Q)
d) 2I(P) = 3I(Q)
Answer: a
Explanation: For a two rotor system, we have L(P)I(P) = L(Q)I(Q)
Now L(P)=2L(Q)
Therefore, 2I(P) = I(Q).
20. In a three rotor system, for the middle rotor, if the stiffness of both the length either side of the rotor is increased to two times what will be the effect on total stiffness of the middle rotor?
a) Remains constant
b) Decreases by two times
c) Increases by two times
d) Increases by 4 times
Answer: c
Explanation: In a three rotor system, each length to either side of the middle rotor is twisted through the same angle therefore the total stiffness is the sum of individual stiffness.
21. Which of the following relation is correct regarding free torsional vibrations of a single motor system?
a) Independent of modulus of rigidity
b) Independent of polar moment of inertia
c) Dependent on mass moment of inertia
d) Independent of length of shaft
Answer: c
Explanation: The free torsional vibrations of a single motor system depends on the following factors:
Modulus of rigidity, Polar moment of inertia, mass moment of inertia and length of the shaft.
22. Free torsional vibrations of a single motor system increases with increase in polar moment of inertia.
a) True
b) False
Answer: b
Explanation: The free torsional vibrations of a single motor system depends on the following factors:
√Polar moment of inertia as directly proportional to the square root of polar moment of inertia.
23. If the polar moment of inertia is increased to four times, then what will be the effect on free torsional vibrations of a single motor system?
a) Increases 4 times
b) Increases 2 times
c) Decreases 4 times
d) Decreases 2 times
Answer: b
Explanation: Since the free torsional vibrations of a single motor system depend on the square root of the polar moment of inertia of the system, increasing 4 times will lead to increase in two times the initial vibration.
24. If the mass moment of inertia is increased to four times, then what will be the effect on free torsional vibrations of a single motor system?
a) Increases 4 times
b) Increases 2 times
c) Decreases 4 times
d) Decreases 2 times
Answer: d
Explanation: Since the free torsional vibrations of a single motor system depend on the inverse of square root of the mass moment of inertia of the system, increasing 4 times will lead to decrease in two times the initial vibration.
25. Calculate the free torsional vibrations of a single motor system from the following data:
C = 8 GN/m2, L=9m, I = 600 Kg-m2, J = 8×104 m4
a) 162,132
b) 172,132
c) 182,132
d) 192,132
Answer: b
Explanation: The free torsional vibrations of a single motor system is given by
12(C.J÷l.I)−−−−−−−−−√
Substituting the given values gives f = 172132 Hz.
26. If the length inertia is decreased to nine times, then what will be the effect on free torsional vibrations of a single motor system?
a) Increases 3 times
b) Increases 9 times
c) Decreases 9 times
d) Decreases 3 times
Answer: a
Explanation: Since the free torsional vibrations of a single motor system depends on the inverse of square root of the length, decreasing 9 times will lead to increase in 3 times the initial vibration.
27. Calculate the Polar moment of inertia in m4 of a single motor system from the following data:
C = 8 GN/m2, L=9m, I = 600 Kg-m2, f=10 Hz
a) 0.00027
b) 0.00032
c) 0.00045
d) 0.00078
Answer: a
Explanation: The free torsional vibrations of a single motor system is given by
12(C.J÷l.I)−−−−−−−−−√
Substituting the given values gives J = 0.00027 m4.
28. If radius of gyration increases then the torsional free vibration increases.
a) True
b) False
Answer: b
Explanation: Increase in the radius of gyration will result in increase in mass moment of inertia since mass moment of inertia is not directly dependent, the given statement is false.
29) Which of the following conditions should be satisfied for static balancing?
1. Dynamic forces acting on the system should be zero
2. Couple acting on the system due to dynamic force should be zero
3. Centrifugal forces acting on the system should be zero
4. Couple acting on the system due to centrifugal forces should be zero
a. Condition 1 and condition 2
b. Condition 1 and condition 3
c. Condition 3 and condition 4
d. All of the above
ANSWER: Condition 1 and condition 3
30) The unbalanced primary couple caused due to reciprocating mass of each cylinder is given as
a. mrlω2 cos θ
b. mrlω (cos θ / n)
c. mrlω2 cos 2θ
d. mrω2 cos 2θ
ANSWER: mrlω2 cos θ
31) Which of the following statements is/are true primary/secondary couple?
1. Secondary couple does not act on V engine
2. Primary couple acts on V engine
3. Secondary couple acts on reciprocating masses of multi-cylinder inline engines
4. Primary couple acts on reciprocating masses of multi-cylinder inline engines
a. 1 and 2
b. 2, 3 and 4
c. 1, 3 and 4
d. All of the above
ANSWER: 1, 3 and 4
32) Which of the following conditions should be satisfied for complete balancing of multi-cylinder inline engines?
a. Primary couples should be balanced
b. Secondary couples should be balanced
c. Both a. and b.
d. None of the above
ANSWER: Both a. and b.
33) At which angle primary unbalanced force in reciprocating engine mechanism is maximum?
a. 0o
b. 90o
c. 360o
d. All of the above
ANSWER: 0o
34) Secondary force in reciprocating engine mechanism is caused due to _______
a. S.H.M. of reciprocating parts
b. oscillation of reciprocating parts
c. obliquity of arrangement of reciprocating parts
d. all of the above
ANSWER: obliquity of arrangement of reciprocating parts
35) The unbalanced force caused due to reciprocating mass is given by the equation
a. mrω2 sin θ + mrω2 (sin 2θ/n)
b. mrω2 sin θ + mrω2 (cos 2θ/n)
c. mrω2 cos θ + mrω2 (cos 2θ/n)
d. mrω2 (sin θ + sin 2θ/n)
ANSWER: mrω2 cos θ + mrω2 (cos 2θ/n)
36) Determine magnitude of balancing mass required if 250 mm is the radius of rotation. Masses of A, B and C are 300 kg, 250 kg and 100 kg which have radii of rotation as 50 mm, 80 mm and 100 mm respectively . The angles between the consecutive masses are 110o and 270o respectively.
a. 45.36 kg
b. 47.98 kg
c. 40.50 kg
d. None of the above
ANSWER: 47.98 kg
37) Which of the following factors are not responsible for unbalancing in rotating systems?
a. Errors
b. Tolerances
c. Shape of the rotor
d. None of the above
ANSWER: None of the above
Prepare For Your Placements: https://lastmomenttuitions.com/courses/placement-preparation/
![]()
/ Youtube Channel: https://www.youtube.com/channel/UCGFNZxMqKLsqWERX_N2f08Q
Follow For Latest Updates, Study Tips & More Content!
Not a member yet? Register now
Are you a member? Login now